Every year, an edition of the ECMAScript Language Specification is released with the new proposals that are officially ready. In practical terms, the proposals are attached to the latest expected edition when they are accepted and reached stage 4 in the TC39 process:

In this article, we’re going to examine and explain the "BigInt" proposal that has been reached stage 4 and belongs to ECMAScript 2020 – the 11th edition.

The content is available as a video as well:

Motivation

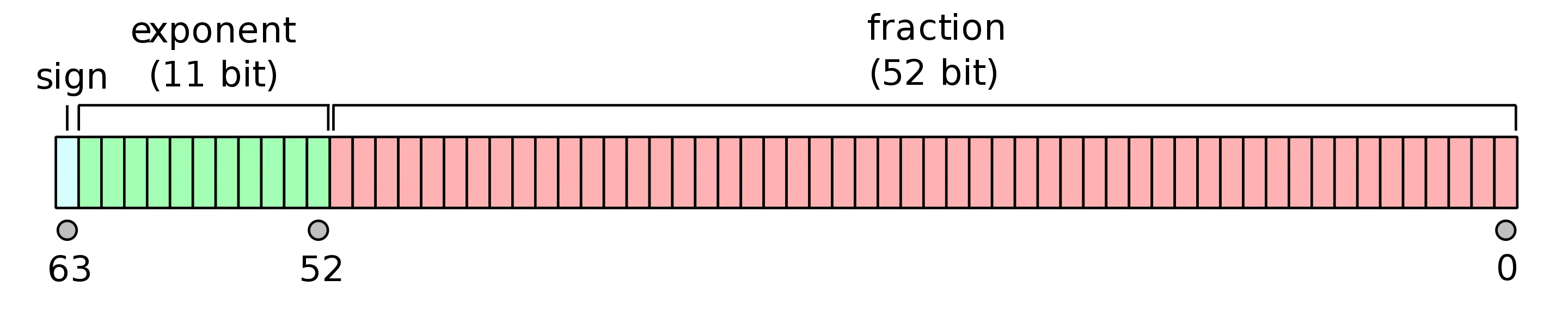
In ECMAScript, Number.MAX_SAFE_INTEGER specifies the maximum safe integer that is acceptable by the engine and is set to 2^53 - 1. This constant arrives from the double-precision floating-point format numbers that the engines use in order to exactly represent numbers and to allow comparing them correctly.

In practice, the number primitive is represented up to 52 explicitly stored bits of the fraction with sign and exponent bits:

Although that most of the time it would be apparently enough, at times, we might need to represent an arbitrarily large integer.

One example from real life, is Twitter IDs, which are unique 64-bit unsigned integers based on timestamps. These IDs overflow the maximum safe integer and to handle that – Twitter decided to represent IDs as strings together with numbers.

Another example is the fs.Stats object in Node.js which practically could hold the same ino value for completely different files (and potentially lead to various bugs):

fs.lstatSync('one.gif').ino // 9851624185071828
fs.lstatSync('two.gif').ino // 9851624185071828 - the same value but a different file  

Indeed, representing arbitrarily large numbers using strings is still an option – but now, with BigInt proposal, there is a true and built-in way to store them in numeric variables.

So, on that note, let’s introduce the proposal.

The Proposal

The proposal specifies a new bigint numeric primitive to represent integers with arbitrary precision larger than 2^53 - 1, which as said, is the maximum safe integer of the number primitive.

The official definition of the specification says:

The BigInt type represents a mathematical integer value. The value may be any size and is not limited to a particular bit-width. Generally, where not otherwise noted, operations are designed to return exact mathematically-based answers.

That is, non-limited integers supporting mathematical operations.

Let’s characterize this primitive.

A New Primitive

A bigint primitive is directly created by appending n suffix to an integer literal:

const bigint = 9007199254740992n;
console.log(bigint); // 9007199254740992n
console.log(typeof bigint); // bigint  

Notice that the type of the operand is actually bigint.

It should be noted that this given numeric literal doesn’t have to be an integer solely – but binary, octal and hexadecimal as necessary:

const bigintAsBinary = 0b100000000000000000000000000000000000000000000000000000n;
console.log(bigintAsBinary); // 9007199254740992n
const bigintAsOctal = 0o400000000000000000n;
console.log(bigintAsOctal); // 9007199254740992n
const bigintAsHexadecimal = 0x20000000000000n;
console.log(bigintAsHexadecimal); // 9007199254740992n  

Moreover, the primitive has an equivalent wrapper object called BigInt allowing to construct it by a given regular integer number or string:

const bigintByNumber = BigInt(Number.MAX_SAFE_INTEGER + 1);
console.log(bigintByNumber); // 9007199254740992n
const bigintByString = BigInt('9007199254740992');
console.log(bigintByString); // 9007199254740992n  

Both given literals could represent the different bases (binary, octal, hexadecimal), although string is capable to exceed Number.MAX_SAFE_INTEGER supposedly.

Operators

Like regular number, basic arithmetic operations are naturally supported:

const addition = 3n + 2n;
console.log(addition); // 5n
const subtraction = 3n - 2n;
console.log(subtraction); // 1n
const multiplication = 3n * 2n;
console.log(multiplication); // 6n
const division = 3n / 2n;
console.log(division); // 1n
const modulo = 3n % 2n;
console.log(modulo); // 1n  

Note that / works as expected, however, it rounds any fractional result towards zero in case of bigint operands.

Also, all of the bitwise operators are supported – including &, |, ^, <<, >> except >>>. Speaking of unsupported operators, unary plus isn’t supported as well to avoid breaking asm.js.

Important to mention that in any case of operation – both operands must be bigint. Meaning, we cannot mix bigint with number:

const invalidOperation = 3n + 2; // TypeError  

And that makes sense, since bigint cannot represent fractions whereas number is limited by a safe integer value. It is noteworthy that we can convert one operand to the other using its wrapper object explicitly and wisely (according to limitations) and so to mix indirectly:

const validOperation = 3n + BigInt(2); // 5n  

Comparisons

We just mentioned that explicit conversions are allowed, and so is abstract equality:

console.log(3n == 3); // true
console.log(3n == '3'); // true
console.log(BigInt(3) == Number(3)); // true
console.log(0n == false); // true  

This means that == behaves as usual when mixing bigint operand with operands from other types. The truth is that the operands of relational operators are mixable as well:

console.log(3n > '2'); // true
console.log(BigInt(3) <= 2); // false  

As to strict equality (===), the result could be true only if both operands are of the same primitive type:

console.log(3n === 3); // false
console.log(3n === '3'); // false
console.log(BigInt(3) === Number(3)); // false
console.log(0n === false); // false  

Summary

We explained in this article the idea behind the “BigInt” proposal and characterized how technically the new primitive can be used.

Let’s sum up:

• The proposal belongs to ECMAScript 2020, which is the 11th edition
• The maximum safe integer for the number primitive is 2^53 - 1
• Representing arbitrarily large numbers, exceed 2^53 - 1, is possible through the string primitive
• The proposal specifies a new built-in bigint numeric primitive
• bigint allows representing integers exceeding 2^53 - 1
• bigint is created by appending n suffix to an integer literal
• bigint has an equivalent wrapper object calledBigInt to construct and operate
• bigint supports basic arithmetic operations such as +, -, *, / and %
• bigint supports both abstract and strict equality comparisons
• bigint supports relational operators

Here’s attached a project with the examples: